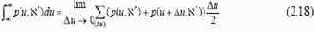Тогда мы можем рассматривать числа
Тогда мы можем рассматривать числа (xi1, xiL, xi2) как треугольные
нечеткие параметры плотности распределения, которая и сама в этом случае
имеет вид нечеткой функции. А зона предельного правдоподобия тогда есть
не что иное, как нечеткий вектор.
Мы видим, что полученное вероятностное распределение имеет не
только частотный, но и субъективный смысл, так как зона предельного
правдоподобия зависит от того, как мы бракуем вероятностные гипотезы.
Представляется, что такое описание всецело отвечает природе
квазистатистики, как мы ее здесь вводим. Чем хуже условия для выдвижения
правдоподобных вероятностных гипотез, чем тяжелее обосновывать такое
правдоподобие, - тем большее значение занимает фактор экспертной оценки.
То вероятностное описание, что мы имеем в итоге, - это гибрид, который
обещает быть плодотворным.
В качестве примера можно рассмотреть нормальный закон
распределения с нечетким среднеквадратическим отклонением (рис. 2.5).
Эта нечеткая функция не имеет полосового вида. И тут самое время
заметить, что функция с треугольными нечеткими параметрами в общем
случае сама не является треугольной и к треугольному виду не приводится.
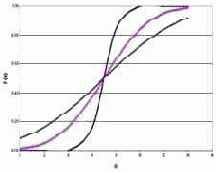
Рис. 2.5. Нормальный закон распределения с нечетким
среднеквадратическим отклонением
Зато выполняется нормировочное условие:
где правая часть представляет собой нечеткое число с вырожденной в точку
функцией принадлежности. Интеграл же, не определенный для не четких
функций общего вида, представляет здесь предел сумм
