ЭВРИСТИЧЕСКИЙ СПОСОБ КОДИРОВАНИЯ
Универсальный способ кодирования редко используется на практике для реализации автоматов с большим числом состояний, поскольку схемы в этом случае получаются весьма сложными за счет большого чсисла элементов памяти. Чаще всего при решении практических задач применяют эвристический способ, основанный на последовательном введении дополнительных состояний и увеличении числа внутренних переменных. В качестве иллюстрации этого способа рассмотрим два примера.
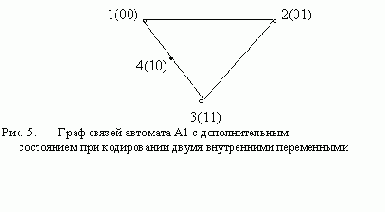
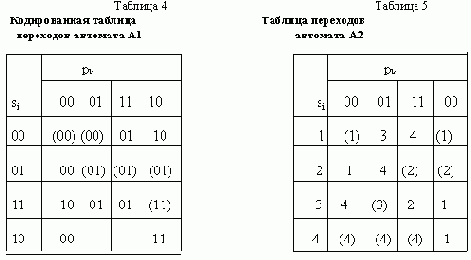
Прежде всего попытаемся реализовать автомат А1 с использованием двух внутренних переменных. Для этого воспользуемся графом связи этого автомата, изображенным на рис. 4,б. Нетрудно убедиться в том, что закодировать такой граф и помощью четырех кодов таким образом, чтобы при каждом переходе изменялось значение только одной переменной, невозможно. Выберем вариант кодирования, при котором наибольшее число переходов выполняется с изменением одной переменной (в нашем примере два перехода), и введем дополнительное состояние для перехода, при котором изменяются две переменные. В результате получаем граф, приведенный на рис. 5. Таблица переходов автомата при таком кодировании изображена в виде табл. 4.
,
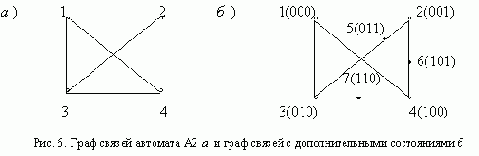
В качестве второго примера рассмотрим кодирование автомата А2, заданного табл. 5. Граф связей этого автомата приведен на рис. 6. Для однозначного кодирования четырех состояний достаточно двух внутренних переменных. Однако выполнить кодирование без состояний с помощью двух переменных оказывается невозможно. Увеличим число внутренних переменных до трех и снова попытаемся произвести кодирование без введения дополнительных состояний.
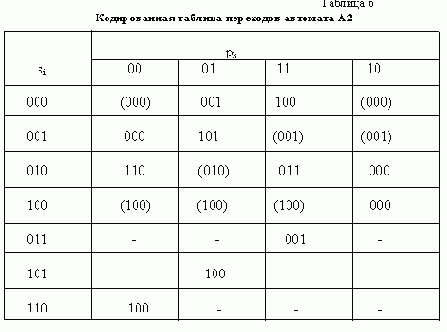
Рассматривая различные варианты, нетрудно убедиться, что получить кодирование без состояний в этом случае также невозможно. Выберем вариант кодирования, позволяющий получить наибольшее число переходов с изменением одной переменной и введем дополнительные состояния. В результате получаем граф автомата, изображенный на рис. 6,б. Используя этот граф, нетрудно построить кодированную таблицу переходов автомата А2 (табл. 6).
В заключение отметим, что описанный универсальный способ кодирвания не является единственным. Например, в работах [1, 3] можно найти описание способа Хаффмэна, который позволяет закодирвать любой автомат, имеющий m состояний, используя 2]log2m[ - 1 элементов памяти, где ]a[ означает ближайшее целое не меньше а. На практике же для построения схем без состояний чаще всего применяют структурный способ, основанный на использовании удвоенного числа элементов памяти. Этот способ будет рассмотрен подробнее в параграфе, посвященном построению элементов памяти, а также в следующем выпуске.
Пред.Страница
След.Страница Раздел Содержание
