Пример построения автомата
Процедуру построения автомата рассмотрим на примере грамматики:
- Г1. 9: R={<E> ®<E> + <T> | <T>,
- <T> ® <T>
* <F> | <F>,
<F> ®
( <E> ) | a}.
- Для искомого автомата имеем:
M3: P = {a, + , * , ) , ( }, H = {E , T , F , a , + , x , ) , h0 , ( }, S = {s0 }, F = {s0}
Для всех правил грамматики строим команды типа (1):
- (1) f0
(s0 , e , E) = {(s0 , T+E) ; (s0 , T)},
(2) f0
(s0 , e , T) = {(s0 , F*T) ; (s0 , F)},
(3) f0
(s0 , e , F) = {(s0 , )E( ) ; (s0 , a)},
Для всех терминальных символов строим команды типа (2):
- (4) f ( s0, a, a ) = ( s0, $ ),
(5) f ( s0 , + , + ) = (s0 , $ ),
(6) f ( s0 , * , * ) = (s0 , $ ),
(7) f ( s0 , ( , ( ) = (s0 , $ ),
(8) f ( s0 , ) , ) ) = (s0 , $ ),
Для перехода в конечное состояние построим команду:
- (9) f (s0 , e
, h0) = ( s0 , $ ).
Построенный автомат является недетерминированным.
Начальную конфигурацию с цепочкой a + a*a запишем так: (s0 , a+a*a , h0E).
Последовательность тактов работы построенного автомата, показывающая, что заданная цепочка допустима, имеет вид:
- (s0 , a+a*a , h0E) |-- (s0 , a+a*a , h0T+E) |--
(s0 , a+a*a , h0T+T) |-- (s0 , a+a*a , h0T+F) |--
(s0 , a+a*a , h0T+a) |-- (s0 , +a*a , h0T+) |--
(s0 , a*a , h0T) |-- (s0 , a*a , h0F*T) |--
(s0 , a*a , h0F*F) |-- (s0 , a*a , h0F*a) |--
(s0 , *a , h0F* ) |-- (s0 , a , h0F) |--
(s0 , a , h0a) |-- (s0 , $ , h0) |--
(s0 , $ , $).
Отметим, что последовательность правил, используемая построенным автоматом, соответствует левому выводу входной цепочки:
E Ю E+T Ю T+T Ю
F+T Ю a+T Ю a+T*F Ю a+F*F Ю a+a*F Ю a+a*a.
Если по такому выводу строить дерево, то построение будет происходить
сверху вниз, т.е. от корня дерева к листьям.
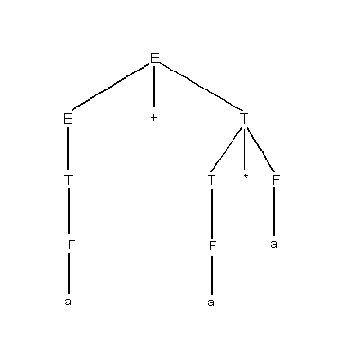
Такой способ построения дерева по заданной цепочке называется нисходящим.
Магазинные автоматы называют часто распознавателями, поскольку они определяют, является ли цепочка, подаваемая на вход автомата, допустимой или нет, и следовательно, отвечают на вопрос, принадлежит ли эта цепочка языку, пораждаемому грамматикой, использованной для построения автомата.
Учитывая характер построения вывода в магазине, автоматы рассмотренного типа называют нисходящими распознавателями.
Еще раз подчеркнем , что доказательство допустимости цепочки нисходящим магазинным автоматом ( НМА) предусматривает поиск определенной последовательности конфигураций.
Такой поиск может существенно увеличить время работы автомата. Детерминированные автоматы не требуют поиска и работают быстрее, поэтому именно такие автоматы применяются на практике. Детерминированные автоматы-распознаватели могут быть построены не для всех, а только для некоторых видов КС-грамматик.
|
Учитывая значение детерминированных автоматов для практических применений, посвятим им последующие разделы.
Пред.Страница
След.Страница Раздел Содержание
